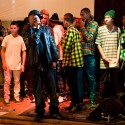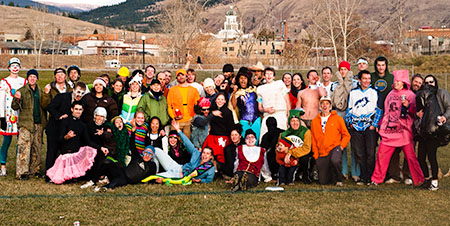Happy Holidays!
Last Thursday I saw Melt Banana play at The Palace. The Lion The Tamer and Deny the Dinosaur? opened. It was my first time at The Palace.
Multnomah and Wahkeenah Falls
On the way drive back to Missoula we stopped to walk a 5 mile loop at the highly recommended Multnomah Falls.
Northwest Jerk Fest 2009
Put on your skinny jeans because its time for Northwest Jerk Fest presented by Northwest Movement Magazine . These are all from the final round featuring Portland’s own Bedrock Boyz vs. The Rip City Jerks.
All you future jerkers out there can learn some new moves here.
Portland to Cannon Beach
On Saturday we drove to the coast. About an hour and a half drive from Portland.
Thanksgiving in Portland
Wednesday evening we drove 550 miles from Missoula to Portland to spend the holiday with Hilary’s friend Kathleen. We crammed a lot into a few days and Kathleen was gracious enough to be our local tour guide. These pictures are from Thanksgiving Day.
The Monty Hall Problem
The Monty Hall Problem is probably the most famous example of how the math of uncertainty can be unintuitive and rather surprising.
Time to use a bit of imagination.
You are a contestant on the game show “Lets Make a Deal” and the host, Monty Hall, presents you with the following scenario:
There are three closed doors up on the stage. One door is hiding shiny new car. All three doors look exactly the same and you have no idea where the car is.
You want that car. You NEED that car.
Monty instructs you to pick one door. After much deliberation you decide door #1.
The game continues:
Monty: “Now, before we open door #1, lets see what’s behind door #3!”
No car. A goat..Interesting.
Now there are two remaining unopened doors, #1 and #2. You know one of them is hiding a car.
The game continues:
Monty: “Do you want to stick with door #1 or switch to door #2?”
Tough choice!
You think: “Should I switch doors? Should I stay? With 2 doors left does it even matter what I do?”
It is common to think that the probability the car is behind either of the remaining doors is one-half you have an equally likely chance of winning no matter what.
The surprising truth is that the preceding thought process is completely wrong. The reality is, loosely speaking, you are twice as likely to win if you switch doors. WTF?
Here’s why:
Before you decide to stay or switch, Monty always reveals a door that does not have the car. This is extremely valuable information!
To see why, think about the beginning of the game and your first choice of doors.
You have a one-third chance of picking the winning door with your initial choice. If this happens and you switch doors, you will end up with a losing door. This is relatively obvious.
Similarly, your chance of picking the wrong door initially is two-thirds. Here, if you switch doors, you will always end up with you winning the car. This fact is subtle and key to understanding this problem.
Remember how we said Monty revealing a losing door was important? If you started with the wrong door, and Monty revealed the other wrong door, then only unopened door left is the one with the car!
What this means is if your original pick was wrong and you then switch to the remaining unopened door, you are guaranteed to win.
It might be helpful to draw a crude picture of 3 doors and see what I am talking about visually.
Since, you are twice as likely to pick a losing door initially, you are twice as likely to win if your strategy is to always switch doors.
Does switching doors guarantee you will win? Unfortunately, no. For an individual game the outcome is always uncertain. In the middle of the game you never know if your initial pick was right or not and there is no way to change this. (bribery?)
The mathematical interpretation of you are “twice as likely to win” means that if you played this game many many many times and switched doors every time, you would win about twice as many games as you would if you played those games and never switched.
The challenging nature of this problem lies in the often unintuitive realm known as conditional probability.
The question is not “What is the probability that I win if I switch doors?”
The exact question is “What is the probability that I will win given that Monty helped me out tremendously by revealing a losing door?”.
Two-thirds! Always switch!
(Don’t get mad at math if you switch doors and end up losing. For that you can thank randomness and uncertainty.)
For more insight on this problem, check out Wikipedia.
Missoula Ultimate Halloween Hat Tournament
Pictures of a rad Saturday in Missoula playing with frisbees.
The the first picture links to a gallery. The last three are pictures that were too big to include.
Holland Lake
We spent last weekend at a forest service cabin near Holland Lake, about halfway between Missoula and Glacier National Park in the Swan Valley.
Saturday we did a 12 mile out and back hike to Upper Holland Lake. The hike had about 2000 feet of elevation gain, which ended up being the difference between fall and winter.
The Mount Vernon Dredge
The Mount Vernon Dredge is an old mining relic located in Nevada City at a history of mining museum. It is a massive structure, kind of reminds me of a brontosaurus when I think about it.
